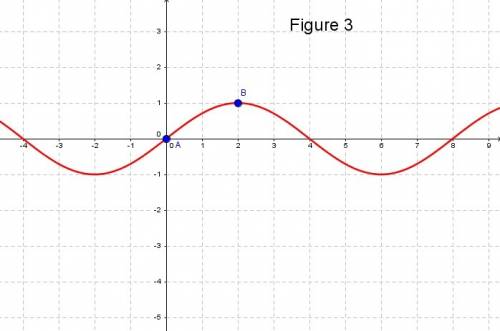
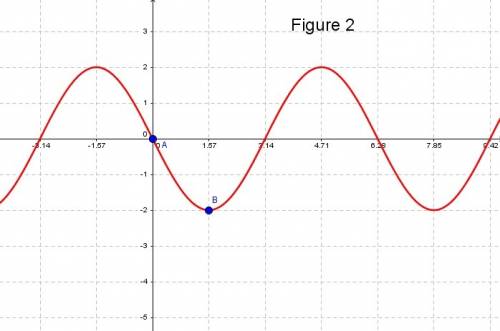
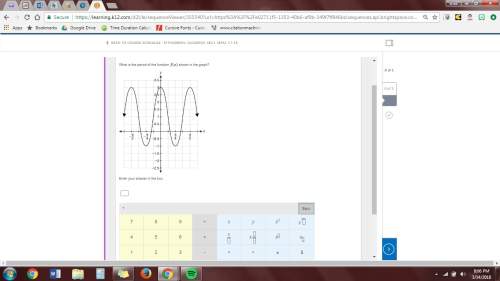
1. what is the period of the function f(x) shown in the graph?
2. (picture)
3. graph th...

Mathematics, 17.10.2019 05:30 hany90
1. what is the period of the function f(x) shown in the graph?
2. (picture)
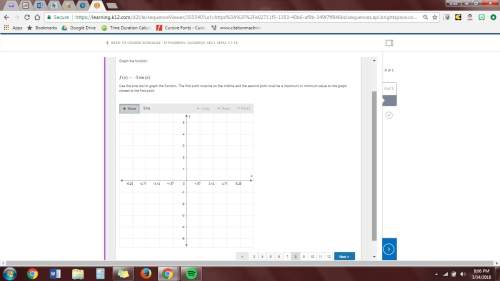
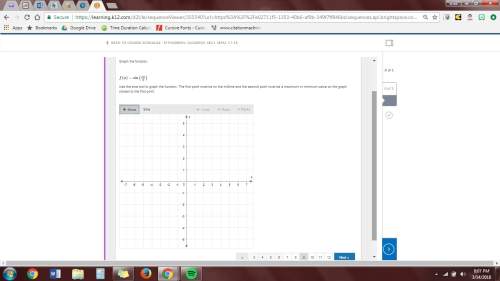
3. graph the function.
f(x)=sin(πx/4)
use the sine tool to graph the function. the first point must be on the midline and the second point must be a maximum or minimum value on the graph closest to the first point.
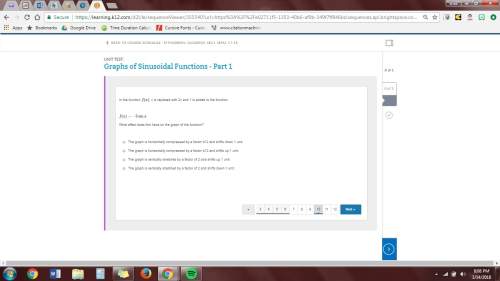
4. in the function f(x), x is replaced with 2x and 1 is added to the function.
f(x)= −3sinx
what effect does this have on the graph of the function?
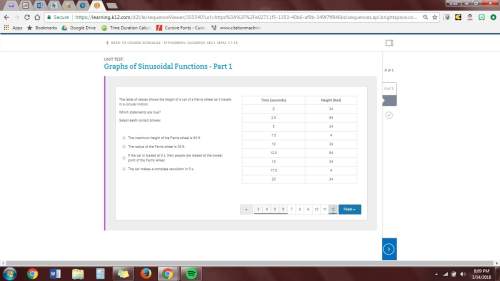
5. over a 24-hour period, the tide in a harbor can be modeled by one period of a sinusoidal function. the tide measures 5.15 ft at midnight, rises to a high of 10.2 ft, falls to a low of 0.1 ft, and then rises to 5.15 ft by the next midnight.
what is the equation for the sine function f(x), where x represents time in hours since the beginning of the 24-hour period, that models the situation?
enter your answer in the box.
6. picture


Answers: 2


Another question on Mathematics

Mathematics, 21.06.2019 13:30
Phillip had some bricks. he stacked them in 6 equal piles. which expression shows the number of bricks phillip put in each pile? let the variable m stand for the unknown number of bricks. m + 6 m÷6 m−6 6m
Answers: 3

Mathematics, 21.06.2019 15:00
When you arrive at the lake, your friend realises he hasn’t got any swimming trunks. you need to ride to a sports shop. the sports shop is 8350 metres away. how many metres is it to cycle there and back?
Answers: 1

Mathematics, 22.06.2019 01:00
For every corresponding pair of cross sections, the area of the cross section of a sphere with radius r is equal to the area of the cross section of a cylinder with radius and height 2r minus the volume of two cones, each with a radius and height of r. a cross section of the sphere is and a cross section of the cylinder minus the cones, taken parallel to the base of cylinder, is the volume of the cylinder with radius r and height 2r is and the volume of each cone with radius r and height r is 1/3 pie r^3. so the volume of the cylinder minus the two cones is therefore, the volume of the cylinder is 4/3pie r^3 by cavalieri's principle. (fill in options are: r/2- r- 2r- an annulus- a circle -1/3pier^3- 2/3pier^3- 4/3pier^3- 5/3pier^3- 2pier^3- 4pier^3)
Answers: 3

Mathematics, 22.06.2019 01:20
Consider the image of klmn for the translation (x, y) → (x – 2, y – 1). what is the ordered pair of l′?
Answers: 1
You know the right answer?
Questions

Mathematics, 13.12.2019 17:31

Mathematics, 13.12.2019 17:31








History, 13.12.2019 17:31




English, 13.12.2019 17:31

Biology, 13.12.2019 17:31

Social Studies, 13.12.2019 17:31

Mathematics, 13.12.2019 17:31