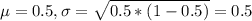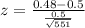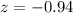Mathematics, 01.07.2021 08:00 selena77
A claim is made that the proportion of 6-10 year-old children who play sports is not equal to 0.5. A
random sample of 551 children aged 6-10 showed that 48% of them play a sport.
For each part below, enter only a numeric value in the answer box. For example, do not type "z =" or "t="
before your answers. Round each of your answers to 3 places after the decimal point.
(a) Calculate the value of the test statistic used in this test.
Test statistic's value
(b) Use your calculator to find the P-value of this test.
P-value =
(c) Use your calculator to find the critical value(s) used to test this claim at the 0.02 significance level. If
there are two critical values, then list them both with a comma between them.
Critical value(s) -

Answers: 3


Another question on Mathematics

Mathematics, 21.06.2019 21:00
Julie buys 2kg of apples and 7kg of pears ? 12.70. the pears cost ? 1.30 per kilogram what is the price per kilogram of the apples? show your working out
Answers: 2

Mathematics, 22.06.2019 01:00
The table shown below gives the approximate enrollment at the university of michigan every fifty years. how many more students were enrolled at the university of michigan in 1950 than in 1900?
Answers: 3

Mathematics, 22.06.2019 01:30
Asample of 200 rom computer chips was selected on each of 30 consecutive days, and the number of nonconforming chips on each day was as follows: the data has been given so that it can be copied into r as a vector. non.conforming = c(10, 15, 21, 19, 34, 16, 5, 24, 8, 21, 32, 14, 14, 19, 18, 20, 12, 23, 10, 19, 20, 18, 13, 26, 33, 14, 12, 21, 12, 27) #construct a p chart by using the following code. you will need to enter your values for pbar, lcl and ucl. pbar = lcl = ucl = plot(non.conforming/200, ylim = c(0,.5)) abline(h = pbar, lty = 2) abline(h = lcl, lty = 3) abline(h = ucl, lty = 3)
Answers: 3

Mathematics, 22.06.2019 01:40
Suppose we have a set of small wooden blocks showing the 26 letters of the english alphabet, one letter per block. (think of scrabble tiles.) our set includes 10 copies of each letter. we place them into a bag and draw out one block at a time. (a) if we line up the letters on a rack as we draw them, how different ways coukl we fill a rack of 5 letters? (b) now suppose we just toss our chosen blocks into a pile, and whenever we draw a letter we already have, we put it back in the bag and draw again. how many different piles of 5 blocks could result? possible? piles will contain at least one repeated letter? (c) if we draw out 5 blocks wit hout looking at them, how many different piles are (d) if we draw out 5 blocks without looking at them, how many of the possible 2. (4) consider the following formula. 12 give two different proofs, one using the factorial formulas and the other combina torial.
Answers: 3
You know the right answer?
A claim is made that the proportion of 6-10 year-old children who play sports is not equal to 0.5. A...
Questions



SAT, 16.02.2022 01:40

History, 16.02.2022 01:40



SAT, 16.02.2022 01:50





SAT, 16.02.2022 01:50

Business, 16.02.2022 01:50


Computers and Technology, 16.02.2022 01:50

Mathematics, 16.02.2022 01:50

Mathematics, 16.02.2022 01:50


Mathematics, 16.02.2022 01:50

Business, 16.02.2022 01:50

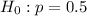
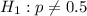
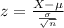
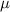 is the value tested at the null hypothesis,
is the value tested at the null hypothesis, 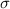 is the standard deviation and n is the size of the sample.
is the standard deviation and n is the size of the sample.