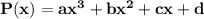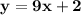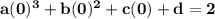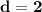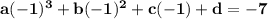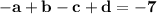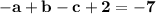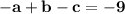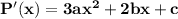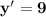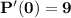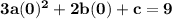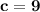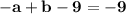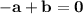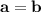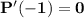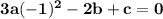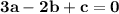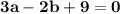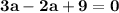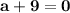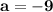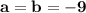Mathematics, 03.10.2019 12:00 rachanachannagiri
The cubic polynomial p(x) = ax^3 + bx^2 + cx + d touches the line with equation y = 9x + 2 at the point (0, 2), and has a stationary point (-1, -7). find p(x)

Answers: 1


Another question on Mathematics

Mathematics, 21.06.2019 20:30
List x1, x2, x3, x4 where xi is the left endpoint of the four equal intervals used to estimate the area under the curve of f(x) between x = 4 and x = 6. a 4, 4.5, 5, 5.5 b 4.5, 5, 5.5, 6 c 4.25, 4.75, 5.25, 5.75 d 4, 4.2, 5.4, 6
Answers: 1

Mathematics, 21.06.2019 21:00
What is the missing statement in step 4? ? rts ? ? vtu and ? rtu ? ? vts ? rts ? ? rvs and ? rtu ? ? stv ? vrs ? ? vru and ? usr ? ? usv ? vur ? ? vus and ? uvs ? ? sru
Answers: 3

Mathematics, 21.06.2019 21:30
Ihave a triangle with a 60 degree angle. lets use d for that angle. what are the values of e and f if d is 60 degrees? and what do you notice about the values of e and f?
Answers: 2

Mathematics, 22.06.2019 01:00
Arrange the steps to solve this system of linear equations in the correct sequence. x + y = -2 2x – 3y = -9 tiles subtract 3x + 3y = -6 (obtained in step 1) from 2x – 3y = -9 (given) to solve for x. substitute the value of x in the first equation (x + y = -2) to get y = 1. the solution for the system of equations is (-3, 1). x = -15 the solution for the system of equations is (-15, 13). add 3x + 3y = -6 (obtained in step 1) to 2x – 3y = -9 (given), and solve for x. x = -3 substitute the value of x in the first equation (x + y = -2) to get y = 13. multiply the first equation by 3: 3(x + y) = 3(-2) 3x + 3y = -6.
Answers: 1
You know the right answer?
The cubic polynomial p(x) = ax^3 + bx^2 + cx + d touches the line with equation y = 9x + 2 at the po...
Questions

Mathematics, 21.12.2020 21:40

Mathematics, 21.12.2020 21:40




Mathematics, 21.12.2020 21:40


Mathematics, 21.12.2020 21:40



Computers and Technology, 21.12.2020 21:40

Mathematics, 21.12.2020 21:40

Mathematics, 21.12.2020 21:40

Mathematics, 21.12.2020 21:40


Mathematics, 21.12.2020 21:40

English, 21.12.2020 21:40



Medicine, 21.12.2020 21:40