
Mathematics, 21.01.2020 18:31 jljhenkel
Recall from class that we found that the fibonacci sequence, with $f_0 = 0$, $f_1 = 1$ and $f_n = f_{n - 2} + f_{n - 1}$, had a closed form $$f_n = \frac{1}{\sqrt{5}} \left( \phi^n - \widehat{\phi}^n \right),$$ where $$\phi = \frac{1 + \sqrt{5}}{2} \; \text{and} \; \widehat{\phi} = \frac{1 - \sqrt{5}}{2}.$$
the lucas numbers are defined in the same way, but with different starting values. let $l_0$ be the zeroth lucas number and $l_1$ be the first. if
\begin{align*}
l_0 & = 2 \\
l_1 & = 1 \\
l_n & = l_{n - 1} + l_{n - 2} \; \text{for}\; n \geq 2
\end{align*}
then what is the tenth lucas number? (note: we seek a numerical answer.)

Answers: 3


Another question on Mathematics

Mathematics, 21.06.2019 18:00
Marla bought a book for $12.95, a binder for $3.49, and a backpack for $44.99. the sales tax rate is 6%. find the amount of tax and the total she paid for these items
Answers: 3

Mathematics, 21.06.2019 19:30
Show your workcan a right triangle have this sides? *how to prove it without using the pythagorean theorema*
Answers: 2

Mathematics, 21.06.2019 22:30
For the chance to be team captain, the numbers 1-30 are put in a hat and you get two chances to pick a number, without replacement. which formula correctly shows how to find the probability that you choose the number 1 and then 2?
Answers: 1

Mathematics, 21.06.2019 23:10
Statements reasons 1. ab ? cd; ad ? bc 1. given 2. ac ? ac 2. reflexive property 3. ? adc ? ? cba 3. ? 4. ? dac ? ? bca; ? acd ? ? cab 4. cpctc 5. ? dac and ? bca are alt. int. ? s; ? acd and ? cab are alt. int. ? s 5. definition of alternate interior angles 6. ab ? cd; ad ? bc 6. converse of the alternate interior angles theorem 7. abcd is a parallelogram 7. definition of parallelogram what is the missing reason in step 3?
Answers: 2
You know the right answer?
Recall from class that we found that the fibonacci sequence, with $f_0 = 0$, $f_1 = 1$ and $f_n = f_...
Questions



Biology, 18.12.2020 22:10

Mathematics, 18.12.2020 22:10


Biology, 18.12.2020 22:10



History, 18.12.2020 22:10

Mathematics, 18.12.2020 22:10




English, 18.12.2020 22:10





English, 18.12.2020 22:10

Physics, 18.12.2020 22:10

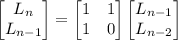
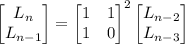
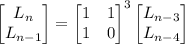

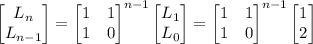
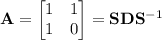 for some matrix
for some matrix 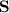 and diagonal matrix
and diagonal matrix 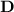 , then
, then 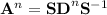 .
.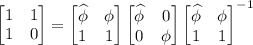
 , you have
, you have





