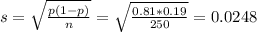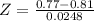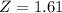Mathematics, 09.04.2021 02:50 cjmann71
Here is a simple probability model for multiple-choice tests. Suppose that each student has probability p of correctly answering a question chosen at random from a universe of possible questions. (A strong student has a higher p than a weak student.) The correctness of an answer to a question is independent of the correctness of answers to other questions. Jodi is a good student for whom p = 0.81.
Required:
a. Use the Normal approximation to find the probability that Jodi scores 77% or lower on a 100-question test.
b. If the test contains 250 questions, what is the probability that Jodi will score 77% or lower?
c. How many questions must the test contain in order to reduce the standard deviation of Jodi's proportion of correct answers to half its value for a 100-item test?
d. Laura is a weaker student for whom p = 0.76. Does the answer you gave in (c) for standard deviation of Jodi's score apply to Laura's standard deviation also?

Answers: 3


Another question on Mathematics

Mathematics, 21.06.2019 14:10
Olivia uses the work below to determine 55% of 720 which explains the error in olivia’s solution
Answers: 1

Mathematics, 21.06.2019 16:00
Planning for the possibility that your home might get struck by lighting and catch on fire is part of a plan
Answers: 1

Mathematics, 21.06.2019 18:00
Find the number of real number solutions for the equation. x2 + 5x + 7 = 0 0 cannot be determined 1 2
Answers: 2

Mathematics, 21.06.2019 20:00
Select the graph of the solution. click until the correct graph appears. |x| = 3
Answers: 2
You know the right answer?
Here is a simple probability model for multiple-choice tests. Suppose that each student has probabil...
Questions

Physics, 20.10.2019 16:20

English, 20.10.2019 16:20


Mathematics, 20.10.2019 16:20


History, 20.10.2019 16:20


Mathematics, 20.10.2019 16:20

Mathematics, 20.10.2019 16:20

English, 20.10.2019 16:20

Spanish, 20.10.2019 16:20

Biology, 20.10.2019 16:20


Social Studies, 20.10.2019 16:20



Chemistry, 20.10.2019 16:20



Mathematics, 20.10.2019 16:20

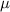 and standard deviation
and standard deviation 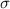 , the z-score of a measure X is given by:
, the z-score of a measure X is given by: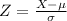
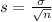 .
.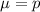 and standard deviation
and standard deviation 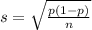
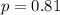
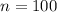
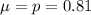
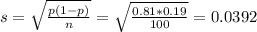
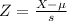
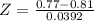
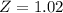
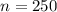 , so:
, so: