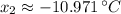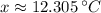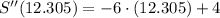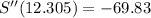Mathematics, 05.11.2020 18:50 GunnerWilbert5178
The number of salmon swimming upstream to spawn is approximated by the following function:
S(x) = -x^3 + 2x^2 + 405x + 4965 where X represents the temperature of the water in degrees Celsius and (6 <= x <= 20
Find the critical value(s) of S(x).
Using the critical values that fall within the domain, apply the 2nd derivative test for the max/min to find the water temperature that produces the maximum number of salmon swimming upstream. (Show work for the 2nd derivative).
The water temperature that produces the maximum number of salmon swimming upstream is degrees Celsius.

Answers: 3


Another question on Mathematics

Mathematics, 21.06.2019 17:00
The table shows the webster family’s monthly expenses for the first three months of the year. they are $2,687.44, $2,613.09, and $2,808.64. what is the average monthly expenditure for all expenses?
Answers: 1

Mathematics, 21.06.2019 17:00
For the rule of 78, for a 12-month period, the last term in the sequence is 12 and the series sums to 78. for an 10 month period, the last term is and the series sum is . for a 15 month period, the last term is and the series sum is . for a 20 month period, the last term is and the series sum is
Answers: 2

Mathematics, 21.06.2019 21:20
In 2009, there were 1570 bears in a wildlife refuge. in 2010, the population had increased to approximately 1884 bears. if this trend continues and the bear population is increasing exponentially, how many bears will there be in 2018?
Answers: 2

Mathematics, 21.06.2019 23:30
Robin spent 25% more time on his research project than he had planned he’s been an extra h ours on the project which of the following expressions could represent the number of hours rob actually spent on the project
Answers: 3
You know the right answer?
The number of salmon swimming upstream to spawn is approximated by the following function:
S(x) = -...
Questions

Mathematics, 25.09.2019 08:30

Mathematics, 25.09.2019 08:30

Spanish, 25.09.2019 08:30




History, 25.09.2019 08:30

Mathematics, 25.09.2019 08:30

Physics, 25.09.2019 08:30


History, 25.09.2019 08:30


History, 25.09.2019 08:30


Mathematics, 25.09.2019 08:30

Mathematics, 25.09.2019 08:30


History, 25.09.2019 08:30

Biology, 25.09.2019 08:30

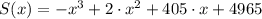 , for
, for 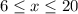 .
.  represents the temperature of the water, measured in degrees Celsius, and
represents the temperature of the water, measured in degrees Celsius, and 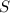 is the number of salmon swimming upstream to spawn, dimensionless.
is the number of salmon swimming upstream to spawn, dimensionless. 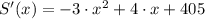 (Eq. 1)
(Eq. 1)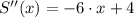 (Eq. 2)
(Eq. 2)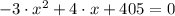
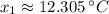 ,
,