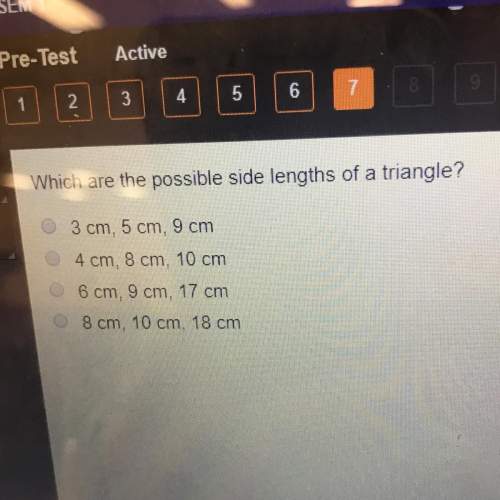
Mathematics, 24.09.2020 14:01 ShadowHedgehog1414
Let ∑k=1[infinity](−1)k+1ak be a convergent alternating series with terms that are nonincreasing in magnitude. Let Rn=S−Sn be the remainder in approximating the value of that series by the sum of its first n terms. Then Rn≤an+1. In other words, the magnitude of the remainder is less than or equal to the magnitude of the first neglected term. For the convergent alternating series ∑k=0[infinity] (−1)k (2k+1)4, evaluate the nth partial sum for n=2. Then find an upper bound for the error S−Sn in using the nth partial sum Sn to estimate the value of the series S.

Answers: 3


Another question on Mathematics

Mathematics, 21.06.2019 17:00
Find the value of the variable and the length of each secant segment.
Answers: 1

Mathematics, 21.06.2019 21:30
Every weekday, mr. jones bikes from his home to his job. sometimes he rides along two roads, the long route that is shown by the solid lines. other times, he takes the shortcut shown by the dashed line. how many fewer kilometers does mr. jones bike when he takes the shortcut instead of the long route?
Answers: 1

Mathematics, 21.06.2019 23:00
Acarton of juice contains 64 ounces miss wilson bought six cartons of juice how many ounces of juice did she buy
Answers: 2

Mathematics, 22.06.2019 02:10
Which pair of expressions is equivalent? a 7(1–k)and7–k b 7(1–k)and1–7k c 7(1–k)and7–k d 7(1–k)and7–7k
Answers: 1
You know the right answer?
Let ∑k=1[infinity](−1)k+1ak be a convergent alternating series with terms that are nonincreasing in...
Questions




Mathematics, 05.05.2020 17:24



History, 05.05.2020 17:24




Business, 05.05.2020 17:24

English, 05.05.2020 17:24








Biology, 05.05.2020 17:24