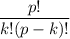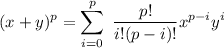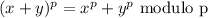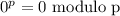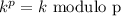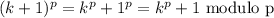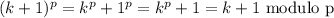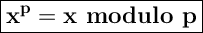Mathematics, 27.08.2020 22:01 kaylastronaut
Let p be a prime number. The following exercises lead to a proof of Fermat's Little Theorem, which we prove by another method in the next chapter. a) For any integer k with 0 ≤ k ≤ p, let (p k) = p!/k!(p - k)! denote the binomial coefficient. Prove that (p k) 0 mod p if 1 ≤ k ≤ p - 1. b) Prove that for all integers x, y, (x + y)^p x^? + y^p mod p. c) Prove that for all integers x, x^p x mod p.

Answers: 2


Another question on Mathematics

Mathematics, 21.06.2019 18:40
Solve the equation below: (x+4)/6x=1/x a. x=2 b. x=0,2 c. x=-2 d. x=0,-2
Answers: 1

Mathematics, 21.06.2019 20:00
Which type of graph would allow us to compare the median number of teeth for mammals and reptiles easily
Answers: 2

Mathematics, 21.06.2019 23:30
Tatiana wants to give friendship bracelets to her 32 classmates. she already has 5 bracelets, and she can buy more bracelets in packages of 4. write an inequality to determine the number of packages, p, tatiana could buy to have enough bracelets.
Answers: 1

Mathematics, 22.06.2019 01:30
Will mark brainliest! ( explain the answer too, it can be one sentence)
Answers: 1
You know the right answer?
Let p be a prime number. The following exercises lead to a proof of Fermat's Little Theorem, which w...
Questions

History, 17.12.2021 05:40




Mathematics, 17.12.2021 05:40


Mathematics, 17.12.2021 05:40

Mathematics, 17.12.2021 05:40

Arts, 17.12.2021 05:40



Mathematics, 17.12.2021 05:40




Computers and Technology, 17.12.2021 05:40



SAT, 17.12.2021 05:40

Social Studies, 17.12.2021 05:40