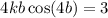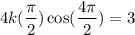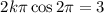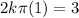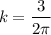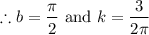Mathematics, 29.07.2020 03:01 cathydaves
Consider the curve of the form y(t) = ksin(bt2) . (a) Given that the first critical point of y(t) for positive t occurs at t = 1 tells us that y '(0) = 1 y(0) = 1 y '(1) = 0 y(1) = 0 Given that the derivative value of y(t) is 3 when t = 2 tells us that y '(3) = 2 y '(0) = 2 y '(2) = 0 y '(2) = 3 (b) Find dy dt = kcos(bt2)·b2t (c) Find the exact values for k and b that satisfy the conditions in part (a). Note: Choose the smallest positive value of b that works.

Answers: 1


Another question on Mathematics


Mathematics, 21.06.2019 17:40
Afamily of five rents a kayak and splits the total time, k, equally. each family member spent less than 25 minutes kayaking. which values can be used to complete the math sentence below so that it accurately represents the situation? intro done
Answers: 2


Mathematics, 21.06.2019 21:00
Ireally need subtract and simplify.(-y^2 – 4y - 8) – (-4y^2 – 6y + 3)show your work, ! i will mark you brainliest but you have to show your work.
Answers: 1
You know the right answer?
Consider the curve of the form y(t) = ksin(bt2) . (a) Given that the first critical point of y(t) fo...
Questions

Geography, 10.03.2021 22:40

Mathematics, 10.03.2021 22:40













History, 10.03.2021 22:40



Mathematics, 10.03.2021 22:40


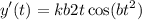
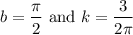
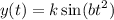
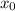 which lies in the domain of f where the derivative is 0.
which lies in the domain of f where the derivative is 0.![y'(t)=\frac{d}{dt}[k \sin (bt^2)]\\ y'(t)=k\frac{d}{dt}[\sin (bt^2)]](/tpl/images/0714/5492/bcd93.png)
![y'(t)=k \cos (bt^2)(\frac{d}{dt}[bt^2])\\ y'(t)=k\cos(bt^2)(b2t)\\ y'(t)= kb2t\cos(bt^2)](/tpl/images/0714/5492/e6dee.png)
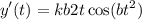
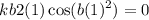
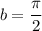
![$\therefore kb2(2)\cos [b(2)^2]=3$](/tpl/images/0714/5492/dd1ee.png)