Use reduction of order (NOT the integral formula we developed) to find the general solution of the nonhomogeneous linear DE, showing all work. Also clearly state the particular solution yp that you obtain using the reduction of order process and show a clear check that your particular solution yp satisfies the original nonhomogeneous DE. [Do NOT use the Method of Undetermined Coefficients here!] ''y + 6y' + 9y + 4e^x
Note: Use the characteristic polynomial to find a first solution yi of the associated homogencous DE.)

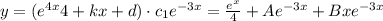where A,B are constants.

Step-by-step explanation:

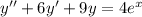Consider the differential equation . To find the homogeneus solution, we assume that 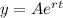and replace it in the equation 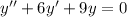. If we do so, after using some properties of derivatives and the properties of the exponential function we end up with the equation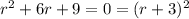

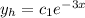which leads to r = -3. So, one solution of the homogeneus equation is , where c_1 is a constant.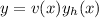

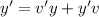
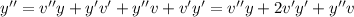
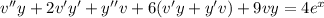
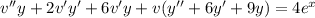
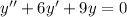To use the order reduction method, assume

where v(x) is an appropiate function. Using this, we get

Plugging this in the original equation we get

re arranging the left side we get

Since y is a solution of the homogeneus equation, we get that . Then we get the equation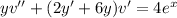

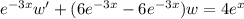
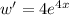
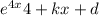We can change the variable as w = v' and w' = v'', and replacing y with y_h, we get that the final equation to be solved is

Or equivalently

By integration on both sides, we get that w = e^{4x}+ k[/tex] where k is a constant.

So by integration we get that v = where d is another constant.

Then, the final solution is

where A,B are constants

according to this law, when unemployment goes up by 1%, gdp drops by 2%. in the question, unemployment rate goes from 2% to 5%, meaning unemployment goes up by 3%, so the gdp drops by 6%. thus the effect is a drop in gdp by 6%.

step-by-step explanation:

hope it you

step-by-step explanation:

sin(7pi/6 - pi/3)  

= sin(7pi/6 - 2pi/6)  

= sin(5pi/6)  

= sin(pi - pi/6)  

= sin(pi/6)  

= 1/2  

sin 7pi/6 - sin pi/3  

= sin (pi + pi/6) - sin pi/3  

= -sin pi/6 - sin pi/3  

= -1/2 - sqrt(3)/2  

= -(1+sqrt(3))2