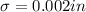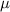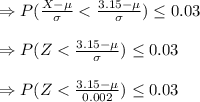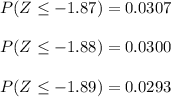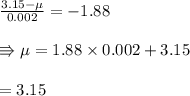Mathematics, 23.06.2020 17:01 seider8952
In a grinding operation, there is an upper specification of 3.150 in. on a dimension of a certain part after grinding. Suppose that the standard deviation of this normally distributed dimension for parts of this type ground to any particular mean dimension LaTeX: \mu\:is\:\sigma=.002 μ i s σ = .002 in. Suppose further that you desire to have no more than 3% of the parts fail to meet specifications. What is the maximum (minimum machining cost) LaTeX: \mu μ that can be used if this 3% requirement is to be met?

Answers: 3


Another question on Mathematics

Mathematics, 21.06.2019 16:00
What is the value of x? enter your answer in the box. x = two intersecting tangents that form an angle of x degrees and an angle of 134 degrees.
Answers: 3

Mathematics, 21.06.2019 17:00
Need this asap if anyone can i would be very grateful. if you could show workings that would really
Answers: 1

Mathematics, 21.06.2019 19:20
Math each whole number with a rational,exponential expression
Answers: 1

Mathematics, 21.06.2019 22:30
Using the figure below, select the two pairs of alternate interior angles.a: point 1 and point 4 b : point 2 and point 3 c: point 6 and point 6d: point 5 and point 7
Answers: 2
You know the right answer?
In a grinding operation, there is an upper specification of 3.150 in. on a dimension of a certain pa...
Questions

Mathematics, 02.06.2021 22:20


History, 02.06.2021 22:20



Computers and Technology, 02.06.2021 22:20





History, 02.06.2021 22:20

Mathematics, 02.06.2021 22:20


Mathematics, 02.06.2021 22:20

Social Studies, 02.06.2021 22:20

Physics, 02.06.2021 22:20

History, 02.06.2021 22:20


English, 02.06.2021 22:20

Computers and Technology, 02.06.2021 22:20