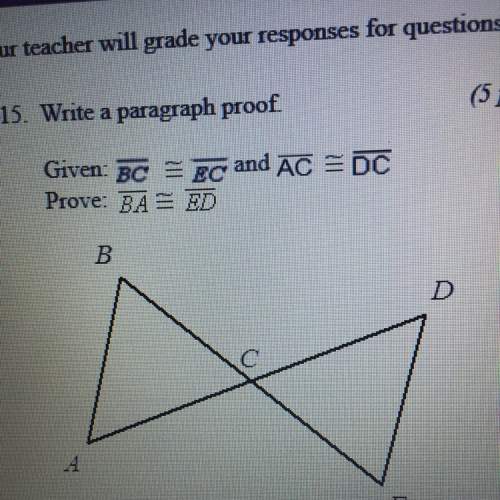
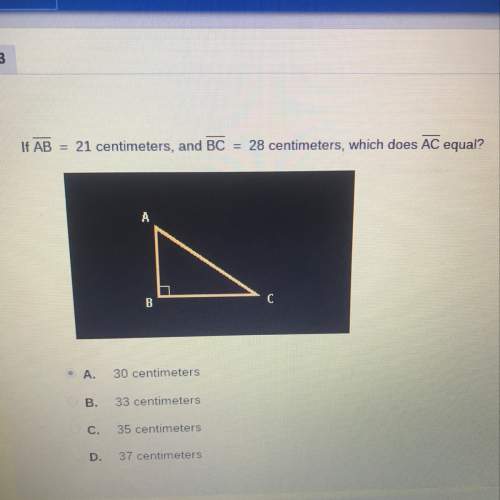
Mathematics, 13.06.2020 01:57 Laners0219
Given $m\geq 2$, denote by $b^{-1}$ the inverse of $b\pmod{m}$. That is, $b^{-1}$ is the residue for which $bb^{-1}\equiv 1\pmod{m}$. Sadie wonders if $(a+b)^{-1}$ is always congruent to $a^{-1}+b^{-1}$ (modulo $m$). She tries the example $a=2$, $b=3$, and $m=7$. Let $L$ be the residue of $(2+3)^{-1}\pmod{7}$, and let $R$ be the residue of $2^{-1}+3^{-1}\pmod{7}$, where $L$ and $R$ are integers from $0$ to $6$ (inclusive). Find $L-R$.

Answers: 1


Another question on Mathematics


Mathematics, 21.06.2019 20:10
Look at the hyperbola graphed below. the hyperbola gets very close to the red lines on the graph, but it never touches them. which term describes each of the red lines? o o o o a. asymptote b. directrix c. focus d. axis
Answers: 3

Mathematics, 21.06.2019 22:30
Need same math paper but the back now i hope your able to read it cleary i need with hw
Answers: 1

You know the right answer?
Given $m\geq 2$, denote by $b^{-1}$ the inverse of $b\pmod{m}$. That is, $b^{-1}$ is the residue for...
Questions


English, 18.09.2021 04:30


Mathematics, 18.09.2021 04:30


Mathematics, 18.09.2021 04:30



Mathematics, 18.09.2021 04:30



Mathematics, 18.09.2021 04:30


English, 18.09.2021 04:30

Biology, 18.09.2021 04:30


Mathematics, 18.09.2021 04:30



Mathematics, 18.09.2021 04:30