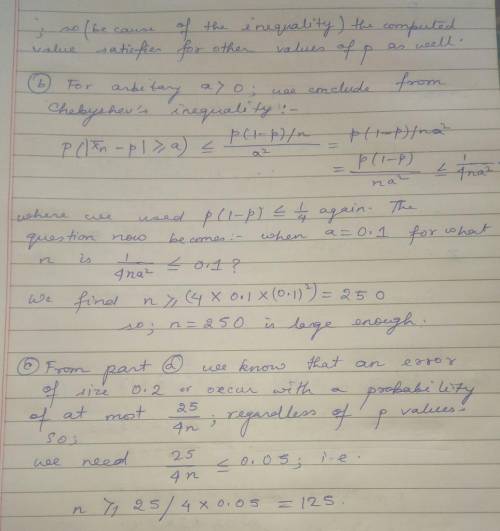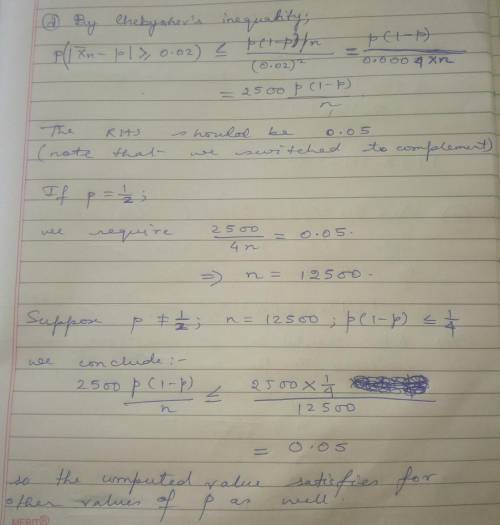Mathematics, 14.04.2020 23:32 adrian08022
The voters in California are voting for a new governor. Of the voters in California, a proportion p will vote for Frank, and a proportion 1 − p will vote for Tony. In an election poll, a number of voters are asked for whom they will vote. Let Xi be the indicator random variable for the event "the ith person interviewed will vote for Frank."1 A model for the election poll is that the people to be interviewed are selected in such a way that the indicator random variables X1, X2, ... are independent and have a Ber(p) distribution. (a) Suppose we use X¯ n to predict p. According to Chebyshev’s inequality, how large should n be (how many people should be interviewed) such that the probability that X¯ n is within 0.2 of the "true" p is at least 0.9? (Hint. solve this first for p = 1/2, and use the fact that p(1 − p) ≤ 1/4 for all 0 ≤ p ≤ 1.) (b) Answer the same question, but now X¯ n should be within 0.1 of p. (c) Answer the question from part (a), but now the probability should be at least 0.95. (d) If p > 1/2, then Frank wins; if X¯ n > 1/2, you predict that Frank will win. Find an n (as small as you can) such that the probability that you predict correctly is at least 0.9, if in fact p = 0.6. 7. Let X1, X2, ..., X144 be independent and identical

Answers: 1


Another question on Mathematics

Mathematics, 21.06.2019 22:30
Amachine that produces a special type of transistor (a component of computers) has a 2% defective rate. the production is considered a random process where each transistor is independent of the others. (a) what is the probability that the 10th transistor produced is the first with a defect? (b) what is the probability that the machine produces no defective transistors in a batch of 100? (c) on average, how many transistors would you expect to be produced before the first with a defect? what is the standard deviation? (d) another machine that also produces transistors has a 5% defective rate where each transistor is produced independent of the others. on average how many transistors would you expect to be produced with this machine before the first with a defect? what is the standard deviation? (e) based on your answers to parts (c) and (d), how does increasing the probability of an event a↵ect the mean and standard deviation of the wait time until success?
Answers: 3

Mathematics, 21.06.2019 23:30
How do you find the distance of each number from the mean
Answers: 1

Mathematics, 21.06.2019 23:30
Consider the sequence below. 3 , 1 , 1/3 , 1/9 , select the explicit function which defines the sequence.
Answers: 1

Mathematics, 21.06.2019 23:30
Graph the line with the given slope m and y-intercept b. m=-3,b=1
Answers: 1
You know the right answer?
The voters in California are voting for a new governor. Of the voters in California, a proportion p...
Questions




Computers and Technology, 30.11.2019 06:31