
Mathematics, 30.03.2020 23:08 lesleyy7278
A test to determine whether a certain antibody is present is 99.1% effective. This means that the test will accurately come back negative if the antibody is not present (in the test subject) 99.1% of the time. The probability of a test coming back positive when the antibody is not present (a false positive) is 0.009. Suppose the test is given to four randomly selected people who do not have the antibody. (a) What is the probability that the test comes back negative for all four people? (b) What is the probability that the test comes back positive for at least one of the four people? (a) Upper P (all 4 tests are negative )equals nothing (Round to four decimal places as needed.)

Answers: 2


Another question on Mathematics

Mathematics, 21.06.2019 17:30
Find the exact value of each of the following. in each case, show your work and explain the steps you take to find the value. (a) sin 17π/6 (b) tan 13π/4 (c) sec 11π/3
Answers: 2

Mathematics, 21.06.2019 19:00
Find the length of the diagonal of the rectangle. round your answer to the nearest tenth. || | | 8 m | | | | 11 m
Answers: 2

Mathematics, 22.06.2019 02:10
Overproduction of uric acid in the body can be an indication of cell breakdown. this may be an advance indication of illness such as gout, leukemia, or lymphoma.† over a period of months, an adult male patient has taken nine blood tests for uric acid. the mean concentration was x = 5.35 mg/dl. the distribution of uric acid in healthy adult males can be assumed to be normal, with σ = 1.87 mg/dl. (a) find a 95% confidence interval for the population mean concentration of uric acid in this patient's blood. what is the margin of error? (round your answers to two decimal places.) lower limit upper limit margin of error (b) what conditions are necessary for your calculations? (select all that apply.) σ is unknown n is large σ is known normal distribution of uric acid uniform distribution of uric acid (c) interpret your results in the context of this problem. there is not enough information to make an interpretation. the probability that this interval contains the true average uric acid level for this patient is 0.05. the probability that this interval contains the true average uric acid level for this patient is 0.95. there is a 95% chance that the confidence interval is one of the intervals containing the population average uric acid level for this patient. there is a 5% chance that the confidence interval is one of the intervals containing the population average uric acid level for this patient. (d) find the sample size necessary for a 95% confidence level with maximal margin of error e = 1.10 for the mean concentration of uric acid in this patient's blood. (round your answer up to the nearest whole number.) blood tests
Answers: 2

Mathematics, 22.06.2019 03:30
Select the correct answer. given: ∆abc with prove: statement reason 1. given 2. ∠cab ≅ ∠edb ∠acb ≅ ∠deb if two parallel lines are cut by a transversal, the corresponding angles are congruent. 3. ∆abc ~ ∆dbe aa criterion for similarity 4. corresponding sides of similar triangles are proportional. 5. ab = ad + db cb = ce + eb segment addition 6. substitution property of equality 7. division 8. subtraction property of equality what is the missing statement in the proof? scroll down to see the entire proof.
Answers: 3
You know the right answer?
A test to determine whether a certain antibody is present is 99.1% effective. This means that the te...
Questions


Chemistry, 01.10.2019 13:10





Mathematics, 01.10.2019 13:10

Health, 01.10.2019 13:10

Mathematics, 01.10.2019 13:10

History, 01.10.2019 13:10

English, 01.10.2019 13:10


Physics, 01.10.2019 13:10


Business, 01.10.2019 13:10




Social Studies, 01.10.2019 13:10

History, 01.10.2019 13:10

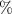 = .991
= .991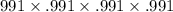 = .9723
= .9723

