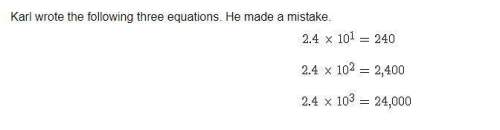This activity will you meet these educational goals:

you will create a quadratic function to model the area of a bean-bag toss carnival game, and then graph it and examine its key features.

your woodworking class is going to make games for the school carnival. you are in charge of making a rectangular game board for a bean bag toss. the length and width of the board have a specific relationship that is shown by the algebraic expressions in the image, which represents a possible finished game board. the units are in inches.
part a
enter the correct answer in the box.
use the expressions that represent the length and width of the game board to write an equation that models the area of the figure. let y represent the area, and write your answer in the form y = ax2 + bx + c, where a, b, and c are real numbers.
part b
graph the equation you wrote in part a. adjust the zoom of the graphing window so the vertex, x-intercepts, and y-intercept can be seen.
part c
the graph of a quadratic equation always has an extreme location (maximum or minimum). state whether the parabola opens upward or downward, whether it has a maximum or a minimum, and what the coordinates of that point are. use the pointer tool to approximate the coordinates of this extreme location to the nearest whole number.
part d
according to the graph, what is the maximum possible area of the game board? give your answer to the nearest whole number. (assume that the maximum area is not reduced by the open hole in the game board.)
part e
type the correct answer in each box.

use the original expressions for the length and width, and substitute the x-coordinate from the extreme location. what are the length and width of the game board at the extreme location?
the length is , and the width is
inches.
part f
what type of quadrilateral will be formed when the game board covers the maximum possible area?
part g
suppose the carnival director asks you to create a game board that is 1,120 square inches. find the dimensions that would meet this request by setting the area equation equal to 1,120, solving for x, and substituting x into the expressions for the length and width. as before, assume the open hole in the game board does not affect the area calculation.
part h
when you solved the area equation for x, did any extraneous solutions result? describe how an extraneous solution would arise in this situation.
part i
what method of solving quadratics did you use to solve the equation set equal to 1,120? why did you choose this method? discuss the usefulness of other methods of solving quadratics as they pertain to this scenario. use this resource to refresh your memory on methods for solving quadratic equations.