When testing gas pumps for accuracy, fuel-quality enforcement specialists tested pumps and found that 1294 of them were not pumping accurately (within 3.3 oz when 5 gal is pumped), and 5705 pumps were accurate. use a 0.01 significance level to test the claim of an industry representative that less than 20% of the pumps are inaccurate. use the p-value method and use the normal distribution as an approximation to the binomial distribution. identify the null hypothesis and alternative hypothesis. a. h0: p=0.2h1: p> 0.2b. h0: p=0.2h1: ≠0.2c. h0: p≠0.2h1: p=0.2d. h0: p> 0.2h1: p=0.2e. h0: p=0.2h1: p< 0.2f. h0: p< 0.2h1: p=0.2the test static is z=the p-value is=because the p-value is (greater than/less than) the significance level (fail to reject/reject) the null hypothesis. there is (sufficient/insufficient) evidence support the claim that less than 20% of the pumps are inaccurate.

E.H0: p=0.2H1: p<0.2

Because the P-Value is (less than) the significance level (reject) the null hypothesis. There is (sufficient) evidence support the claim that less than 20% of the pumps are inaccurate.

Step-by-step explanation:

1) Data given and notation

n=1294+5705=6999 represent the random sample taken

X=1294 represent the number of pumps that were not pumping accurately

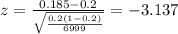
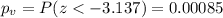
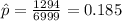estimated proportion of pumps that were not pumping accurately

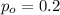is the value that we want to test

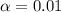represent the significance level

Confidence=99% or 0.99

z would represent the statistic (variable of interest)

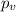represent the p value (variable of interest)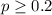  

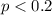
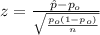2) Concepts and formulas to use  

We need to conduct a hypothesis in order to test the claim that that less than 20% of the pumps are inaccurate:  

Null hypothesis:  

Alternative hypothesis:  

E.H0: p=0.2H1: p<0.2

When we conduct a proportion test we need to use the z statistic, and the is given by:  

(1)  

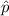The One-Sample Proportion Test is used to assess whether a population proportion is significantly different from a hypothesized value .

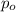3) Calculate the statistic  

Since we have all the info requires we can replace in formula (1) like this:  

4) Statistical decision  

It's important to refresh the p value method or p value approach . "This method is about determining "likely" or "unlikely" by determining the probability assuming the null hypothesis were true of observing a more extreme test statistic in the direction of the alternative hypothesis than the one observed". Or in other words is just a method to have an statistical decision to fail to reject or reject the null hypothesis.  

The significance level provided . The next step would be calculate the p value for this test.  

Since is a one left tailed test the p value would be:  

Because the P-Value is (less than) the significance level (reject) the null hypothesis. There is (sufficient) evidence support the claim that less than 20% of the pumps are inaccurate.

idk

step-by-step explanation: