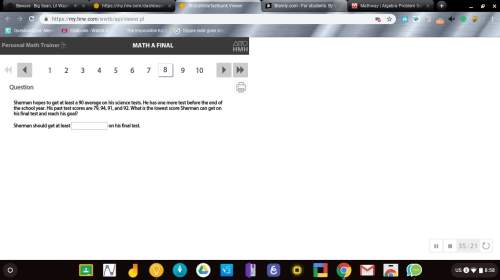
Mathematics, 29.11.2019 05:31 bay62
We now have lim x → [infinity] (4x − ln(x)) = lim x → [infinity] 4x 1 − ln(x) 4x . let's first focus on lim x → [infinity] ln(x) 4x . since ln(x) → [infinity] as x → [infinity], then this limit is indeterminate of type [infinity]/[infinity]. using l'hospital's rule, we find: lim x → [infinity] ln(x) 4x = lim x → [infinity] 1 = 0 .

Answers: 1


Another question on Mathematics

Mathematics, 21.06.2019 20:30
Angles r and s are complementary. the measure of angle r is 31 degrees. which equation can be used to find angle s?
Answers: 1

Mathematics, 21.06.2019 23:00
Acompany made a profit of 75000 over a period of 6 years on an initial investment of 15000 what is the annual roi
Answers: 1


Mathematics, 22.06.2019 03:00
Si el duplo del mayor de dos numeros se divide entre el el triplo del menor, el cocient es 1 y el residuo 3, y si 8 veces el menor se divide por el mayor, el cociente es 5 y el residuo 1
Answers: 1
You know the right answer?
We now have lim x → [infinity] (4x − ln(x)) = lim x → [infinity] 4x 1 − ln(x) 4x . let's first focus...
Questions


Mathematics, 03.11.2020 22:10





Chemistry, 03.11.2020 22:10

Mathematics, 03.11.2020 22:10

Mathematics, 03.11.2020 22:10


Mathematics, 03.11.2020 22:10


Biology, 03.11.2020 22:10

English, 03.11.2020 22:10

Mathematics, 03.11.2020 22:10

Chemistry, 03.11.2020 22:10

Physics, 03.11.2020 22:10


English, 03.11.2020 22:10

Mathematics, 03.11.2020 22:10