Compute the second partial derivatives ∂2f ∂x2 , ∂2f ∂x ∂y , ∂2f ∂y ∂x , ∂2f ∂y2 for the following function. f(x, y) = 2xy (x2 + y2)2 , on the region where (x, y) ≠ (0, 0) verify the following theorem in this case. if f(x, y) is of class c2 (is twice continuously differentiable), then the mixed partial derivatives are equal; that is, ∂2f ∂x ∂y = ∂2f ∂y ∂x .

Answer with step-by-step explanation:

We are given that a function

Differentiate partially w.r.t x

Then, we get

Differentiate again w.r.t x

Differentiate function w.r.t y

Again differentiate w.r.t y

Differentiate partially w.r.t y

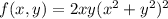
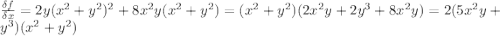
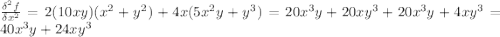
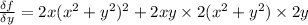
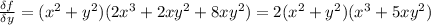
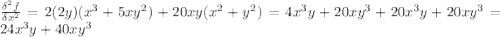
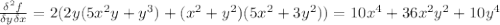
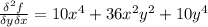
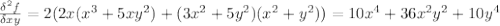
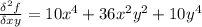
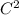Hence, if f(x,y) is of class (is twice continuously differentiable), then the mixed partial derivatives are equal.

i.e

a

step-by-step explanation: