
Mathematics, 30.07.2019 09:10 levelebeasley1
Why do the parametric equations x(t)=-cos(t) and y(t)=2sin(2t) equal the cartesian equation (x^2)+(1/2)y=1?
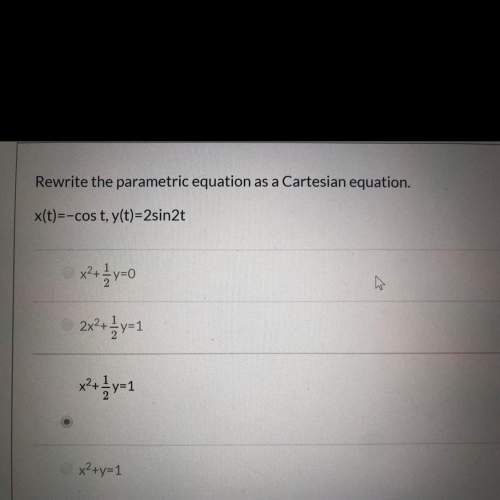

Answers: 2


Another question on Mathematics

Mathematics, 21.06.2019 16:00
Find the amount in a continuously compounded account for the given condition. principal: $1000, annual interest rate: 4.8%, time: 2 yr
Answers: 3


Mathematics, 21.06.2019 21:50
6x + 3y = -6 2x + y = -2 a. x = 0, y = -2 b. infinite solutions c. x = -1, y = 0 d. no solution
Answers: 1

Mathematics, 21.06.2019 22:30
Sketch the vector field vector f( vector r ) = 8vector r in the xy-plane. select all that apply. the length of each vector is 8. the lengths of the vectors decrease as you move away from the origin. all the vectors point away from the origin. all the vectors point in the same direction. all the vectors point towards the origin. the lengths of the vectors increase as you move away from the origin.
Answers: 2
You know the right answer?
Why do the parametric equations x(t)=-cos(t) and y(t)=2sin(2t) equal the cartesian equation (x^2)+(1...
Questions

Mathematics, 28.01.2020 02:31

Spanish, 28.01.2020 02:31


English, 28.01.2020 02:31


Mathematics, 28.01.2020 02:31


Mathematics, 28.01.2020 02:31

Mathematics, 28.01.2020 02:31


Mathematics, 28.01.2020 02:31



Social Studies, 28.01.2020 02:31

Health, 28.01.2020 02:31

Mathematics, 28.01.2020 02:31

Mathematics, 28.01.2020 02:31


Mathematics, 28.01.2020 02:31

Mathematics, 28.01.2020 02:31




