
Mathematics, 03.11.2019 12:31 yayrocks2395
The equations that must be solved for maximum or minimum values of a differentiable function w=f(x, y,z) subject to two constraints g(x, y,z)=0 and h(x, y,z)=0, where g and h are also differentiable, are gradientf=lambdagradientg+mugradien th, g(x, y,z)=0, and h(x, y,z)=0, where lambda and mu (the lagrange multipliers) are real numbers. use this result to find the maximum and minimum values of f(x, y,z)=xsquared+ysquared+zsquared on the intersection between the cone zsquared=4xsquared+4ysquared and the plane 2x+4z=2.

Answers: 3


Another question on Mathematics

Mathematics, 21.06.2019 14:40
The physical fitness of an athlete is often measured by how much oxygen the athlete takes in (which is recorded in milliliters per kilogram, ml/kg). the mean maximum oxygen uptake for elite athletes has been found to be 60 with a standard deviation of 7.2. assume that the distribution is approximately normal.
Answers: 3

Mathematics, 21.06.2019 20:30
Is the point (0, 8) on the x-axis or y-axis? how do you know?
Answers: 2


You know the right answer?
The equations that must be solved for maximum or minimum values of a differentiable function w=f(x,...
Questions

Biology, 17.12.2020 20:20


Mathematics, 17.12.2020 20:20


Mathematics, 17.12.2020 20:20

English, 17.12.2020 20:20

Arts, 17.12.2020 20:20

Mathematics, 17.12.2020 20:20


Chemistry, 17.12.2020 20:20

Chemistry, 17.12.2020 20:30

Mathematics, 17.12.2020 20:30

Mathematics, 17.12.2020 20:30

Biology, 17.12.2020 20:30


Health, 17.12.2020 20:30


Mathematics, 17.12.2020 20:30

Mathematics, 17.12.2020 20:30

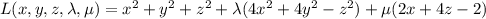
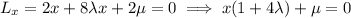
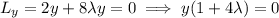
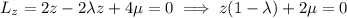
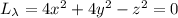
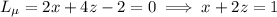
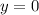 , then
, then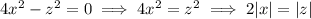

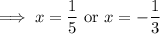
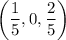 and
and 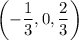
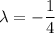 , then in the first equation we get
, then in the first equation we get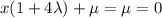
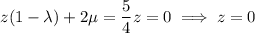
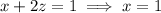
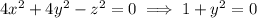
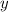 , so this case yields no additional critical points.
, so this case yields no additional critical points.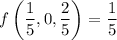 (min)
(min)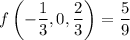 (max)
(max)

