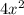Mathematics, 24.06.2019 13:00 24chrim
Write a polynomial function of minimum degree with real coefficients whose zeros include those listed. write the polynomial in standard form. 5, -3, and -1 + 3i f(x) = x4 + 12.5x2 - 50x - 150 f(x) = x4 - 4x3 + 15x2 + 25x + 150 f(x) = x4 - 4x3 - 15x2 - 25x - 150 f(x) = x4 - 9x2 - 50x - 150 question 13(multiple choice worth 5 points) use the rational zeros theorem to write a list of all potential rational zeros. f(x) = x3 - 7x2 + 9x - 24 ±1, ±2, ±3, ±4, ±6, ±8, ±12, ±24 ±1, ±2, ±3, ±4, ±24 ±1, ±one divided by two, ±2, ±3, ±4, ±6, ±8, ±12, ±24 ±1, ±2, ±3, ±4, ±6, ±12, ±24 question 14(multiple choice worth 5 points) perform the requested operation or operations. f(x) = 7x + 6, g(x) = 4x2 find (f + g)(x). 7x + 6 + 4x2 28x3 + 24x 7x + 6 - 4x2 seven x plus six divided by four x squared. will give great feedbback and will give best answer brainliestasap

Answers: 1


Another question on Mathematics

Mathematics, 21.06.2019 19:30
When 142 is added to a number the result is 64 more times the number my options are 35 37 39 41
Answers: 1

Mathematics, 21.06.2019 20:00
In one day there are too high tides into low tides and equally spaced intervals the high tide is observed to be 6 feet above the average sea level after six hours passed a low tide occurs at 6 feet below the average sea level in this task you will model this occurrence using a trigonometric function by using x as a measurement of time assume the first high tide occurs at x=0. a. what are the independent and dependent variables? b. determine these key features of the function that models the tide: 1.amplitude 2.period 3.frequency 4.midline 5.vertical shift 6.phase shift c. create a trigonometric function that models the ocean tide for a period of 12 hours. d.what is the height of the tide after 93 hours?
Answers: 1

Mathematics, 21.06.2019 20:00
In new york city at the spring equinox there are 12 hours 8 minutes of daylight. the longest and shortest days of the year very by two hours and 53 minutes from the equinox in this year the equinox falls on march 21 in this task you use trigonometric function to model the hours of daylight hours on certain days of the year in new york city a.what is the independent and dependent variables? b.find the amplitude and the period of the function. c.create a trigonometric function that describes the hours of sunlight for each day of the year. d. graph the function you build in part c. e. use the function you build in part c to find out how many fewer daylight hours february 10 will have than march 21. you may look at the calendar.
Answers: 1

You know the right answer?
Write a polynomial function of minimum degree with real coefficients whose zeros include those liste...
Questions


English, 08.03.2021 07:40

English, 08.03.2021 07:40

Health, 08.03.2021 07:40

Mathematics, 08.03.2021 07:40


Mathematics, 08.03.2021 07:40


Mathematics, 08.03.2021 07:40

Arts, 08.03.2021 07:40


Mathematics, 08.03.2021 07:40

Chemistry, 08.03.2021 07:40

Mathematics, 08.03.2021 07:40





Business, 08.03.2021 07:40

Spanish, 08.03.2021 07:40

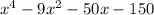
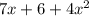
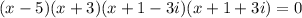
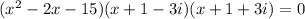
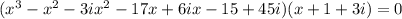
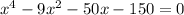
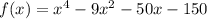 .
. is a zero of p(x) = 0. Then, p is a factor of the constant term of p(x) and q is a factor of the leading coefficient of p(x)'.
is a zero of p(x) = 0. Then, p is a factor of the constant term of p(x) and q is a factor of the leading coefficient of p(x)'.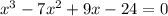 . Then, p is a factor of -24 and q is a factor of 1.
. Then, p is a factor of -24 and q is a factor of 1.